题目：中小微企业的信贷决策

背景：银行首先根据中小微企业的实力、信誉对其信贷风险做出评估，然后依据信贷风险等因素来确定是否放贷及贷款额度、利率和期限等信贷策略。

附件：包含有/无信贷记录的企业信息

主要解决下列问题：

(1) 对附件1中123家企业的信贷风险进行量化分析，给出该银行在年度信贷总额固定时对这些企业的信贷策略。

通过对大量文献资料的研读, 确立了“利润总额”“发票有效比”“变异系数”“供求关系稳定度” “信誉等级”五个衡量信贷风险的指标, 并建立了基于 TOPSIS 方法的信贷风险综合评价模型。同时，在兼顾了利润最大和风险最低的情况下，本文通过线性规划的方法，给出了一套银行在年度信贷总额固定时对这些企业的信贷策略.

(2) 在问题1的基础上，对附件2中302家企业的信贷风险进行量化分析，并给出该银行在年度信贷总额为1亿元时对这些企业的信贷策略。

先进行因子分析，确定输入变量，DNN回归预测（预测信誉评级）

(3) 企业的生产经营和经济效益可能会受到一些突发因素影响，而且突发因素往往对不同行业、不同类别的企业会有不同的影响。综合考虑附件2中各企业的信贷风险和可能的突发因素（例如：新冠病毒疫情）对各企业的影响，给出该银行在年度信贷总额为1亿元时的信贷调整策略。

参考过去3年内的绩优行业指数基金的净值波动(爬虫)以弥补新冠肺炎稀缺的定量研究数据，经过计算得出在新冠病毒疫情这一突发事件下各行业的波动情况，以此分析出该突发因素对各行业造成的影响，本文依据该影响情况对上述的信贷策略进行了修正，给出了银行在年度信贷总额为1亿元时的信贷调整策略.

附件****1 123家有信贷记录企业的相关数据

附件****2 302家无信贷记录企业的相关数据

附件3 银行贷款年利率与客户流失率关系的2019年统计数据

模型建立

信贷风险量化模型的建立

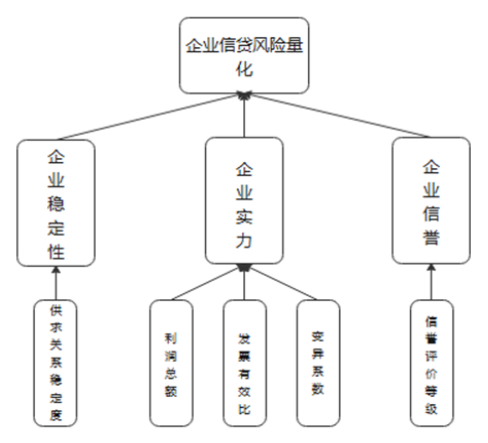
指标权重的确立

主观: 层次分析法(AHP)需要专家打分

基于数据:熵值法
方法如下:

step1:初始指标规范法处理

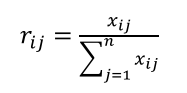
step2:指标熵值计算

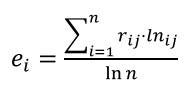
step3:权重指标计算
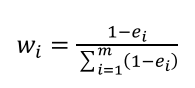
原理

在信息论中，熵是对不确定性的一种度量。信息量越大，不确定性就越小，熵也就越小.我们可以用熵值来判断某个指标的离散程度，指标的离散程度越大，该指标对综合评价的影响（权重）越大，其熵值越小

基于熵权的TOPSIS模型

TOPSIS 常用于对多指标的模型评价构建, 并且已经得到广泛应用, 但在传统应用过程中, 权重的确定要么设定为相同, 要么由专家确定, 难以避免因其主观性而产生的误差. 因此, 我们决定采用上述的熵值法所得的熵权对 TOPSIS 模型进行修正, 建立一个基于熵权的 TOPSIS 模型, 以此来减小主观性因素在信贷风险量化的影响.
- TOPSIS模型简介
  1. 应用场景:能够根据现有的数据，对个体进行评价排序,与AHP不同的是:AHP的应用场景是在没有明确的量化指标的情况下，而topsis是在有量化指标的情况下完成的.举例:在医院检查身体，医生最后会给每个人体检报告，上面有你的一些和健康相关的指数，在这种有实实在在数字支持的时候，如何较为客观的评价大家的健康状况就是我们要研究的问题.
  2. 基本原理
    
    TOPSIS中文名称就是优劣解距离法,简单理解:一个指标到该指标的最优解的距离越小说明越好.但实际来看会更复杂,比如往往会有多个指标来决定一个结果的好坏,但有些指标越大(小)越好,有些指标越接近某个值越好.因此还需要一系列处理步骤来综合考虑这些因素
- 1.数据正向化: 将不同类型的数据都转化成越大越好
  
  数据分类及转化方法如下:
  - 极大型指标（效益类指标）：指标数值越大越好。
  - 极小型指标（成本类指标）：指标数值越小越好。
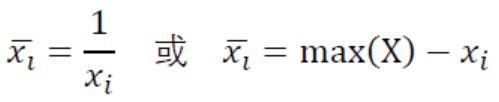
  - 中间型指标：指标数值越接近某个值越好。
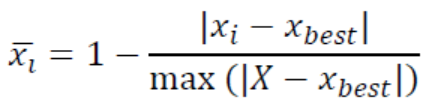
  - 区间型指标：指标数值在某个区间范围内最好，区间中的数值大小无优劣之分
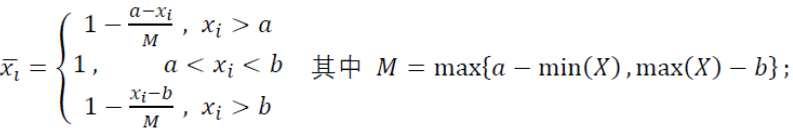
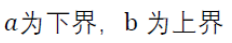
- 2.标准化:去除量纲影响
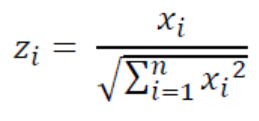
- 3.评分构建
  
  分别找出每个指标的最大最小值,构建两个最优方案集合.其中到最优解的距离记为D+，到最劣解的距离记为D-，最终的评价指标,其中C越接近于1，就说明这个更优.
- 4.增加权重：在计算D+D-时进行加权